(1) 확실한 지식? 2020. 3. 3.
(2) 기하학적 사유의 확실성 – 1. 2020. 3. 3.
(3) 기하학적 사유의 확실성 – 2. 2020. 3. 10.
(4) 포르투나와 사피엔티아, 또는 확률적 사유. 2020. 3. 17.
(5) 19세기의 과학과 수학. 2020. 3. 24.
(6) 하이젠베르크의 불확정성 원리. 2020. 3. 31.
(7) 거짓말쟁이의 역설과 양자역학의 서울 해석. 2020. 4. 7.
(8) 수학기초론과 괴델의 불완전성 정리. 2020. 4. 14.
(9) 인식론의 문제. 2020. 4. 21.
(10) 과학과 수학은 확실한 지식을 주는가? 2020. 4. 21.
글: 김재영 (녹색아카데미)
대상적/통계적 확률 개념이 본격적으로 영향력을 미치기 시작한 것은 19세기의 일이었다. 벨기에의 천문학자이자 수학자였던 아돌프 케틀레는 천문학에서 오차를 평가하고 분석하는 방법으로 사용되던 통계학적 접근을 사회적인 문제로 확장했다.
케틀레가 1835년 출간한 『인간과 그 능력의 개발에 관한 논고: 사회물리학 시론』은 천문학에서 자주 사용되는 통계적 및 확률적 접근을 이용하여 사회적인 현상들을 다루려는 야심찬 학문적 시도이다.

‘사회물리학’(physique sociale)에서 가장 중요한 개념은 ‘평균인’(l’homme moyen)이었다. 사회현상은 대단히 복잡하고 서로 긴밀하게 얽혀 있어서 이성적인 접근이 힘든 것처럼 보이지만, 천문학에서 성공적으로 사용되고 있는 ‘오차의 법칙’, 즉 정규분포의 이론을 원용한다면, 사회현상도 천문학처럼 과학적으로 서술할 수 있다는 것이다.
사회를 구성하는 각 개인의 판단과 행위를 일일이 확인하고 예측하는 것은 실질적으로 전혀 불가능한 일이지만, 각 개인을 천문학(또는 수학)의 평균 개념에 대응하는 추상적 개념인 ‘평균인’으로 대치한다면, 복잡한 사회현상도 모두 확실한 지식의 영역으로 넘어올 것이라고 케틀러는 믿었다.
사회현상에 통계학과 확률이론을 적용하는 ‘사회물리학’의 프로그램은 생물학과 물리학에 직접적인 영향을 미쳤다. 19세기에서 두드러진 물리학적 발전 중 하나는 열역학의 성립이다. 물이나 기체에 열을 가하면 온도나 압력이나 부피가 달라지며, 물이 수증기로 바뀌기도 하고 얼음이 되기도 하는데, 이것이 열적 현상이다.

열역학은 열적 현상에 대한 경험적인 법칙들을 실험실에서의 정교한 관찰을 통해 확립하려는 노력을 집대성한 것이다. 즉 이러한 경험적 법칙들로부터 더 일반적인 수준에서 적용될 수 있으며 열적 현상에 보편적으로 적용되는 것으로 여겨지는 법칙들을 구성하고 이 법칙들로부터 개별현상을 설명하고 예측할 수 있게 하는 이론이 열역학이다. 그러나 열역학은 뉴턴의 고전역학에 비해 그 기초가 분명하지 않았다.
뉴턴의 고전역학은 천문학적 현상뿐 아니라 가장 작은 물체의 운동까지 모든 것에 적용될 수 있는 근본적인 이론체계로 자리를 잡았지만, 열역학의 법칙들은 임의적인 것처럼 보였으며, 훨씬 더 보편적인 것으로 여겨지는 뉴턴역학과 어떤 관계에 있는지 밝혀낼 필요가 있었다.
열역학을 더 기본적인 뉴턴의 고전역학으로부터 유도하려는 노력에서 가장 중심적인 역할을 한 것은 확률이론이었다. 즉, 확률이론을 원용하여 고전역학의 근간이 되는 ‘미시상태’ 대신에 ‘거시상태’를 쓴다면 열역학에서 기술하는 현상론적 법칙을 모두 유도할 수 있다는 것이다. 이것이 통계역학이다.
통계역학은 기체분자운동론에 그 기원을 두고 있다. 다니엘 베르누이를 비롯하여 헤러퍼쓰(1821), 워터스턴(1846), 크뢰니히(1856), 클라우지우스(1857) 등과 같은 일련의 선구적인 학자들은 기체에 대한 현상론적 법칙을 원자론적으로 설명하고자 했다. 다시 말해 일정한 부피를 차지하고 있는 상자 안에 있는 기체가 일정한 온도를 유지하고 있을 때 그 상자의 벽에 가해지는 압력을 계산할 수 있게 하는 법칙을 원자론적으로 설명하고자 했다.

이를 위해 그들은 기체는 일정한 성질을 갖는 분자(원자 또는 입자)로 이루어져 있다는 가정 아래 분자들 사이의 상호작용(충돌 등)의 결과로 기체의 압력, 온도, 부피 등이 정해짐을 밝혔다. 이는 곧 분자들 전체의 모임이 나타내는 현상을 개개 분자들에 대한 동역학으로부터 유도하려는 노력이었다. 다시 말해서, 거시적 현상을 미시적 기본이론으로 설명하려는 것이었다.
열역학은 여러 현상론적 법칙들을 포괄하는 더 일반적인 수준의 네 가지 법칙들에서 출발한다. 그러나 이 역시 더 기본적인 이론으로부터 ‘유도’될 수 있는가 하는 문제가 기체분자운동론의 연구자들의 과제였다. 19세기에 더 기본적인 이론이란 다름 아니라 뉴턴-라그랑쥬-해밀턴의 역학체계를 가리킨다.
통계역학이 부딪힌 첫 문제 중 하나는 열역학 둘째 법칙과 통계역학적 접근을 화해시키는 일이었다. 열역학 둘째 법칙은 계의 상태변화에 방향성이 있음을 주장한다. 기다란 금속막대 한쪽을 뜨겁게 달구었다고 하자. 시간이 흐르면 한쪽 끝은 뜨겁고 다른 쪽 끝은 차가운 처음 상태는 금속막대 전체가 같은(또는 비슷한) 온도로 미지근해지는 나중 상태로 이행하며, 그 반대는 성립하지 않는다.

방안 한 구석에 있는 풍선 속에 몰려 있던 기체들은 풍선을 터뜨리면 어느 정도 시간이 흐른 뒤 방안 전체에 골고루 퍼지게 되며, 그 반대는 성립하지 않는다. 이와 마찬가지로 더 뜨거운 온도의 열기관은 더 차가운 온도로 되면서 외부에 일을 해 주지만, 그 반대로 더 차가운 온도의 열기관이 주변에서 일을 모아 저절로 더 뜨거워지는 일은 생기지 않는다.
이것이 열역학 둘째 법칙의 기본 내용이다. 비슷한 예로서, 큰 상자 속에 흰 바둑돌과 검은 바둑돌을 얇은 막으로 나누어 왼쪽 절반에는 모두 흰 바둑돌이, 오른쪽 절반에는 모두 검은 바둑돌이 있게 한 뒤에, 갑자기 얇은 막을 제거하고 상자 전체를 오랫동안 흔들면, 결국 두 종류의 바둑돌들이 모두 골고루 섞이게 된다. 그러나 반대로 골고루 섞여 있는 두 종류의 바둑돌이 들어 있는 상자를 오랫동안 흔들어도 결국 흰 바둑돌과 검은 바둑돌이 반반씩 구분되어 놓이는 일은 발생하지 않는다.
열역학 둘째 법칙을 정량적으로 표현하면, 엔트로피라 부르는 양이 있어서 열역학적 계의 상태의 변화는 항상 엔트로피가 감소하지 않는 방향으로 일어난다고 말할 수 있다. 현상의 변화과정에 명백하게 방향이 있다고 말하는 것은 이론에서 비롯했다기보다는 관찰에서 비롯된 것이다.

맥스웰과 볼츠만은 기체가 ‘분자’(molecule)로 이루어져 있으며 거시적으로 나타나는 기체의 상태들은 모두 분자들의 통계적인 분포에 따라 정해진다는 이론을 발전시켰다. 이 과정에서 베르누이 이후의 접근과 달리 확률의 개념이 명시적으로 도입되었다.
열역학 둘째 법칙은 열역학 첫째 법칙과 달리 통계적으로만 또는 확률론적으로만 성립하는 법칙이며, 그렇기 때문에 엔트로피가 감소하는 것은 절대적이지 않다. 열현상을 기술하는 방정식만으로는 상태변화에 방향성이 있다는 것을 설명할 수 없다.
금속판을 구성하는 분자들 중에서 더 느리게 움직이는 분자들이 오른쪽 반으로 몰리고, 더 빠르게 움직이는 분자들이 왼쪽 반으로 몰리면 미지근한 온도로 열평형상태에 있는 금속판의 오른쪽 끝은 차가와지고 왼쪽 끝은 뜨거워지게 된다. 다만 확률적으로 이러한 분자들의 수는 그 반대의 경우에 비해 압도적으로 적다.
상자 속의 두 종류의 바둑돌이 섞이는 확률은 두 종류의 바둑돌이 상자 속에서 반반씩 각각 나뉘어 놓이게 될 확률보다 압도적으로 크다. 이런 의미에서 열역학 둘째 법칙은 확률적인 법칙이다.

볼츠만은 미시적인 역학에서 나타나는 가역성과 거시적 열역학에서 나타나는 비가역성 사이의 상충을 해결하기 위해 H정리를 유도했다. 이 정리가 로슈미트와 체르멜로의 혹독한 비판에 부딪히자 볼츠만은, “원자론적 견해에 따르면, 열역학의 둘째법칙은 단지 확률이론의 정리 중 하나에 불과하다”고 주장했다.
눈에 보이는 운동에 대해서는 H정리에서 주장하는 바와 같은 비가역성이 나타날 수 없다는 것이 명백하지만, 대단히 많은 수의 매우 작은 분자들이 개입해 있는 운동에서는 확률이 더 작은 상태에서 확률이 더 큰 상태로의 전이가 항상 있어야 한다는 것이다.
이는 조사이어 깁스의 “외부의 엔트로피를 증가시키지 않고 엔트로피가 감소하는 것이 불가능하다는 것은 확률의 문제로 환원되는 것으로 보인다.”는 결론과 일맥상통하는 것이다. 요컨대, 기체분자운동론 또는 그 확장된 형태로서의 통계역학에서는 현상의 기술에서 확률개념의 도입이 필수적임을 매우 잘 보여주는 역사적 사례라 할 것이다.
그런데 흥미롭게도 볼츠만이 H정리와 관련된 로슈미트와 체르멜로와의 논쟁에 대답하기 위해 내세운 확률이론 또는 확률계산의 규칙(Wahrscheinlichkeitsrechnung)은 형식적으로는 정립된 체계이지만, 그 철학적/인식론적 함의에 대한 논의는 완결되어 있지 않은 이론이다. 어떤 의미에서는 양자역학에서와 비슷하게, 볼츠만은 통계역학의 인식론적 함의에 대한 논의를 모두 확률 개념의 인식론적 함의에 대한 논의로 떠넘겼다고 할 수 있다.
19세기에 확률과 통계의 개념을 도입함으로써 근본적인 변화를 겪은 것은 물리학만의 상황이 아니었다. 생물학에서도 통계적 사고는 혁명적이었다. 생기론과 기계론의 논쟁이나 목적론과 본질론의 대립에서 확률 개념이 중요한 역할을 했다.
19세기 생물학에서 나타나는 확률적 및 통계적 사고의 영향은 일방적인 것이 아님을 강조한다. 아직 확률이론이나 통계학도 제 자리를 찾아가는 과정 중에 있었기 때문에, 통계학 개념의 발전 과정에서 생물학적 문제들이 중요한 역할을 하는 경우가 많았다.
가령 우생학으로 널리 알려져 있는 프랜시스 골턴이 생물학자일 뿐 아니라 통계학자이기도 한 것은 그런 이유에서이다. 기거렌쩌 등이 공동으로 저술한 『우연의 제국: 확률이 어떻게 과학과 일상생활을 바꾸었는가?』(1989)에서 생물학과 확률적 사고의 관계는 생리학, 자연학, 유전학, 진화론의 네 가지 측면에서 요약된다.
먼저 생리학에서는 자연발생과 조절의 문제가 확률적 사고와 연결된다. 프랑스의 클로드 베르나르처럼 결정론을 옹호하는 생리학자들은 자연발생적인 것처럼 보이는 생리현상들도 겉으로 보기에만 그런 것이지 사실은 그 뒤에 감추어져 있는 메커니즘이 존재한다고 믿었다.
독일의 에른스트 헤켈이나 칼 에른스트 폰베어와 같은 발생학 또는 자연학의 맥락에서는 기계론자라 하더라도 우연을 충분히 용인할 수 있었다. 폰베어는 물리학과 화학만으로는 생명현상, 특히 개체의 발생이나 환경에 따라 개체가 변화하는 과정을 설명할 수 없음을 지적하고, 생명의 본질이 내재함을 주장했다.

그레고르 멘델이 잡종의 유전을 연구할 때 사용한 방법은 통계적인 것이었다. 통계적이라는 것은 현상 속에서 다양한 상관관계를 밝혀내고 정리하는 데 목표를 둔다. 이것은 개별적인 대상들에서 실제로 일어나고 있는 인과적인 사건들에 주목하는 것과 대비된다.
찰스 다윈이 『종의 기원』(1859)에서 주목한 것은 생물체들이 모여 있는 곳에서는 변이가 언제나 나타난다는 점이었다. 케틀레가 사회현상을 이해하기 위해 추상적 개념으로서의 ‘평균인’에 주목한 것과 달리 다윈은 변이에 초점을 맞추었다. 생명의 조건이 변화함에 따라 늘 있게 마련인 변이에서 더 잘 적응하여 살아남는 것이 있으며, 오랜 시간이 지나게 되면 이러한 변이들의 중심축이 옮겨가는 것이 자연선택이다.
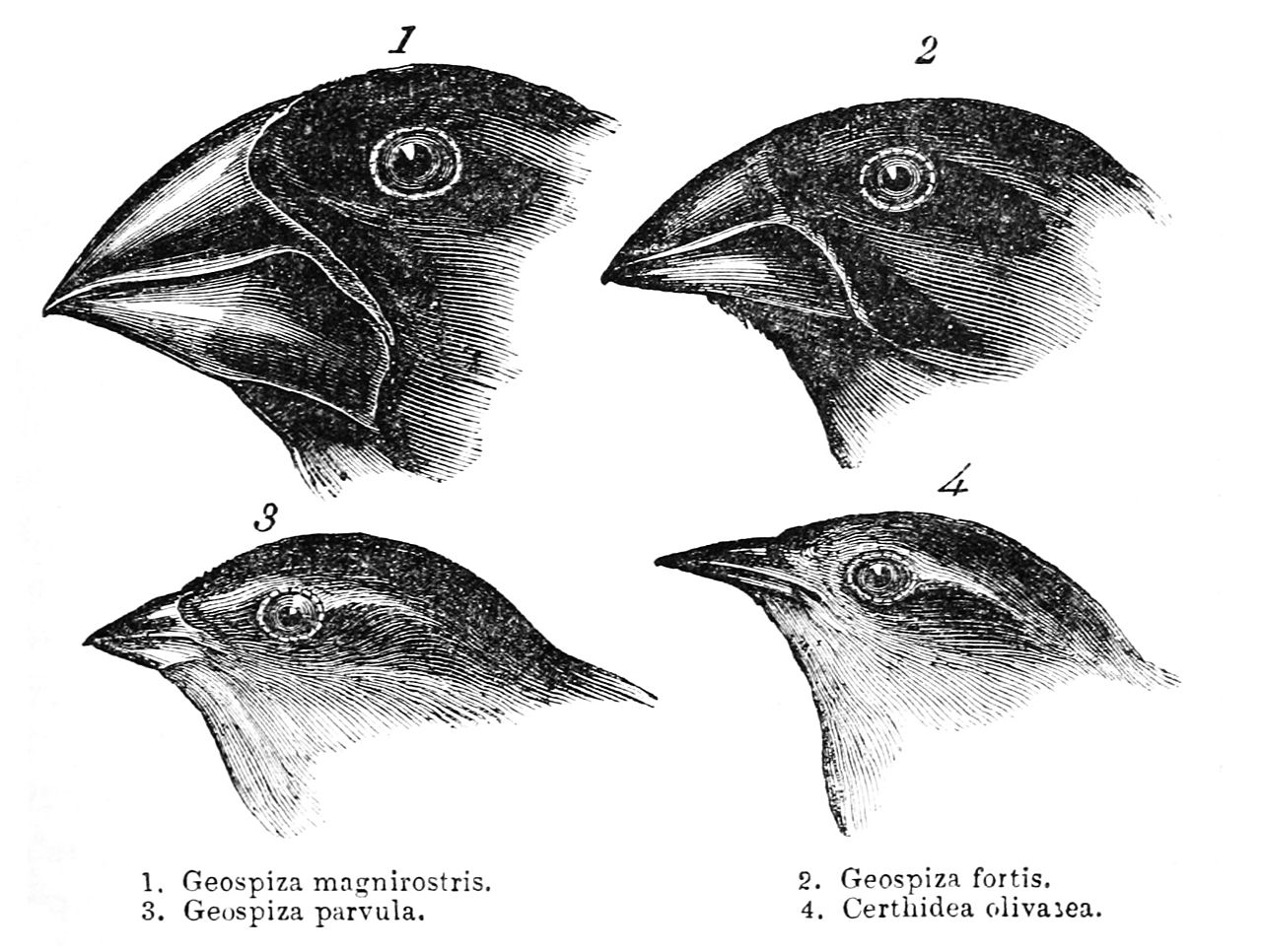
요컨대 19세기에 최대로 불거져 나온 확률적 및 통계적 사유는 물리과학과 생명과학에서 오히려 전혀 기대하지 않았던 커다란 혁신을 낳았다. 이러한 접근이 아니었다면 여전히 18세기적인 좁은 기하학적 사유에서 벗어나지 못하고 있었을 것이다.
여기에서 다루지는 않지만 19세기 동안 에우클레이데스의 기하학 체계에서 제5의 공리, 즉 평행선 공리를 포기함으로써 근본적으로 새로운 모습을 갖추게 된 비유클리드 기하학들은 오히려 유클리드 기하학의 아름다움과 엄밀성을 더 부각시켜 주었을 뿐 아니라 평행선 공리의 위치도 재평가할 수 있게 해 주었음에 주목할 필요가 있다.
(6) 하이젠베르크의 불확정성 원리로 이어집니다.
과학칼럼은 매주 화요일에 업로드됩니다.
참고문헌
- 김재영. (2001). “한계로서의 확률: 양자역학과 통계역학의 예”, 『과학과 철학』, 제12집. pp. 1~20.
- 김재영. (2004). “통계역학의 기초 다시 보기: 메타동역학적 접근”, 『과학철학』, 제7권 pp. 21~63.
- 김재영. (2010). “불확실성의 과학은 어떻게 만들어졌는가?”. 박성민 외, 『불확실한 세상』 사이언스북스. pp. 251-284.
- 야마오카 에쓰로 (2004). 『거짓말쟁이의 역설』, 안소현 옮김, 영림카디널.
- 장회익 외 (2016). 『양자, 정보, 생명』 한울아카데미.
- Franzén, Torkel (2005). Gödel’s Theorem. An Incomplete Guide to Its Use and Abuse. A K Peters.
- Gigerenzer, G. et al. (1989). The Empire of Chance: How probability changed science and everyday life. Cambridge University Press.
- Goldstein, R. (2005). Incompleteness: The proof and paradox of Kurt Gödel. Norton; 고중숙. (2007). 『불완전성: 쿠르트 괴델의 증명과 역설』, 승산.
- Hacking, I. (1975). The emergence of probability: A philosophical study of early ideas about probability, induction and statistical inference. Cambridge University Press.
- Harman, P. (19 ). Energy, Force, Matter: Physics in the Nineteenth Century. Harvard University Press; 김동원, 김재영 (2000). 『에너지, 힘, 물질: 19세기의 물리학』, 성우출판사.
- Kline, M. (1982). Mathematics: The Loss of Certainty. Oxford University Press; 심재관. (2007). 『수학의 확실성: 불확실성 시대의 수학』, 사이언스북스.
*알림: 웹사이트 스킨 문제로 댓글쓰기가 안되고 있습니다. 댓글이나 의견 등은 녹색아카데미 페이스북 그룹, 트위터, 인스타그램 등을 이용해주시면 감사하겠습니다. 공부모임 게시판에서는 댓글을 쓰실 수 있습니다. 이용에 불편을 드려 죄송합니다. – 녹색아카데미 greenacademy.kr@gmail.com
